2010. 9. 5. 16:00ㆍ프로그래밍일반
삼각함수의 이해 - 1
>> 들어가기에 앞서
우리가 흔히 삼각함수라고 하면 중학교 때부터 주구장창 학습해 오던 내용이기에 너무 쉬운 주제가 아닐까라는 의문을 가질 수도 있겠지만, 미적분과 선형대수, 일반물리를 비롯해서 각종 이공계 분야에서 삼각함수의 어마어마한 활용범위를 생각한다면 오히려 첫 강좌에서 가볍게 다루고 넘어가기에는 부족하다는 느낌이 들 정도이다. 따라서 우선 첫 강좌에서는 삼각함수의 기초적인 내용들을 복습해 보고, 추후 필요에 따라서 각 강좌의 주제에 맞게 다시 언급하도록 하겠다.
>> 피타고라스의 정리 (Pythagorean theorem)
삼각함수는 간단히 말하자면 직각삼각형의 각 변의 비율을 정의해둔 함수인데, 이에 대한 본격적인 내용의 진행에 앞서서 직각삼각형에 대한 너무나도 유명한 정리인 피타고라스 정리에 대해 가볍게 복습해 보고 넘어가자. 직각삼각형을 다루는데 있어서 피타고라스 정리가 빠지면 무언가 좀 섭섭해진다.

표1에서 알아본 피타고라스의 정리를 잘 이용하면 직각삼각형의 두 변의 길이를 알 때 나머지 한 변의 길이를 구하는 문제는 간단한 대수적 조작에 불과함은 별도의 설명이 필요 없을 것이다. 그리고 피타고라스의 정리에 대해서는 역사적으로 워낙 많은 연구가 행해졌기 때문에 그 증명방법이 수백여 가지에 이른다고 하는데, 우리도 피타고라스의 정리를 증명하는 간단한 대수적 방법 한 가지를 예제로써 풀어보고 넘어가도록 하자.

>> 삼각함수(Trigonometric Function)의 정의
이제 본격적으로 삼각함수에 대해서 살펴보자. 우선 삼각함수를 대표하는 사인, 코사인, 탄젠트 함수 및 이들의 역수로 정의되는 코시컨트, 시컨트, 코탄젠트의 정의를 알아보는 것으로부터 삼각함수에 대한 논의를 시작해 보자. 이들 6개의 함수가 바로 삼각함수의 기본함수이다.
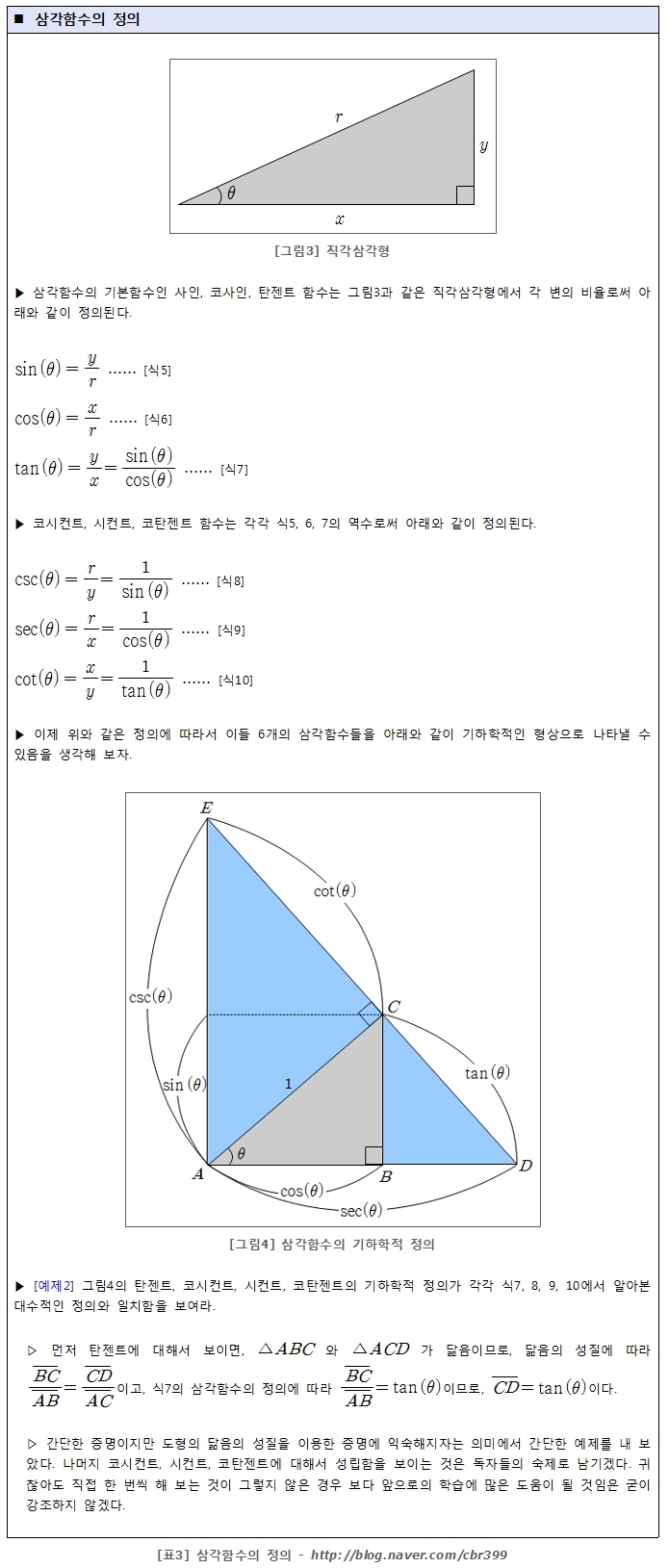
이제 직각삼각형에 대한 각 변의 비율을 표3과 같은 삼각함수들로 정의해 둔 이유는 무엇인지, 또는 이런 삼각함수의 뛰어난 활용성이 과연 어디에 있는지 등에 대해서는 계속되는 절에서 알아보도록 하자.
>> 좌표값 변환에서 삼각함수의 활용
우리는 표3을 통해서 6개의 대표적인 삼각함수의 정의에 대해서 알아보았다. 삼각함수의 정의에서는 표3과 같이 직각삼각형의 각 변의 비를 사용하지만, 사실 삼각함수는 직각삼각형 보다는 원과 더욱 밀접한 관련이 있다는 점을 이해할 수 있어야 한다. 즉, 이 말은 삼각함수가 반지름이 r인 원의 원점으로부터 원위의 각 점으로 향하는 벡터를 각도의 매개변수 방정식으로 나타내고자 할 때 유용하게 활용될 수 있음을 의미한다.
나중에 선형대수를 공부하고 벡터방정식에 대해서 공부하게 되면 보다 명확해 지겠지만, 현 시점에서 잘 이해가 가지 않는다면 간단히 극좌표계에서 직교좌표계로의 좌표값 변환을 떠올려 보면 이해가 쉬울 것이다. 이에 대해서 좀 더 명확히 이해하기 위해서 아래와 같은 간단한 예제를 풀어보고 넘어가도록 하자.

표4의 예제3을 통해서 삼각함수를 활용하면 각도가 0~360도로 변하는 동안 반지름이 r인 원위의 모든 점의 좌표를 구할 수 있음을 이해했을 것이다. 이것이 바로 원위의 모든 점의 자취를 따르는 벡터에 대한 각도의 매개변수 방정식인데, 이에 대한 자세한 내용은 선형대수와 미적분을 공부하고 난 뒤, 벡터미적분을 다룰 때 다시 언급할 기회가 있을 것이다.
그리고 나중에 일반물리학을 공부하게 되면 알게 되겠지만, 이런 좌표값 변환에서의 삼각함수의 활용이라는 것은 결국 뉴턴 역학에 의한 힘의 벡터량을 우리가 관심을 가지는 좌표계의 각 기저에 대한 방향으로 분리하고자 할 때 응용된다는 것을 자연스럽게 깨닫게 될 것이다. 이에 대해서는 나중에 일반물리를 공부할 때 다시 언급하도록 하겠다.
>> 삼각함수의 특수한 값들
대부분의 삼각함수의 값은 무리수의 형태로 나타나지만, 특수한 각에 대해서는 유리수의 형태로 나타낼 수 있는데, 학창시절 "삼각함수의 특수한 값들"이라는 이름의 테이블을 외웠던 기억이 있을 것이다. 표4에서 알아본 좌표값 변환에서의 삼각함수의 활용이라는 이해와 함께 사인 30도의 값이 0.5임을 증명하는 것 따위를 포함해서 이들 특수한 값들을 간단히 유도할 수 있음을 알아보도록 하자.

이와 같이 원위의 한 점에 대한 좌표값 변환과 밀접한 관련이 있다는 삼각함수의 의미와 사인30도에 대한 증명만 기억하고 있으면 표5에서 알아본 삼각함수의 특수한 값들은 외울 필요 없이 언제든지 가볍게 유도할 수 있음을 기억하도록 하자.
>> 강좌를 마치며
시간 관계상 첫 강좌는 여기에서 마무리하도록 하고, 다음 강좌에서 계속해서 삼각함수와 관련된 기초적인 내용들을 복습하는 시간들을 이어가도록 하겠다. 앞으로 선형대수와 미적분, 일반물리에서는 물론이고 3D그래픽스 응용에 있어서도 삼각함수는 지겹도록 자주 사용하게 될 것이다. 따라서 만약 현 시점에서 삼각함수에 대해 익숙하지 않아서 다소 혼란스럽다면 삼각함수와 친해질 때까지 계속해서 머릿속으로 그 정의와 활용도를 생각해 주는 것이 앞으로의 학습에 많은 도움이 될 수 있을 것이다.
출퇴근길에서, 화장실에서, 식사시간에 등등 하루를 보내며 별 다른 의미없이 지나칠 수 있는 여러 짜투리 시간들을 활용해서 습관적으로 자신이 공부하는 내용을 머릿속으로 떠올려 주는 것이 공부에 많은 도움이 된다는 사실은 내가 경험을 통해서 깨닫게 된 진리이다. 따라서 이를 믿고 실천해 보는 것이 공부와 친해지는 좋은 방법이 될 것이다.
[출처] 삼각함수의 이해 - 1 (2010-09-07 강의노트)|작성자 프로포즈